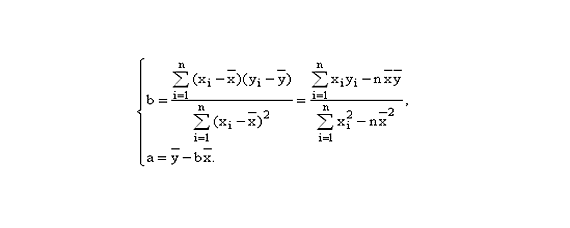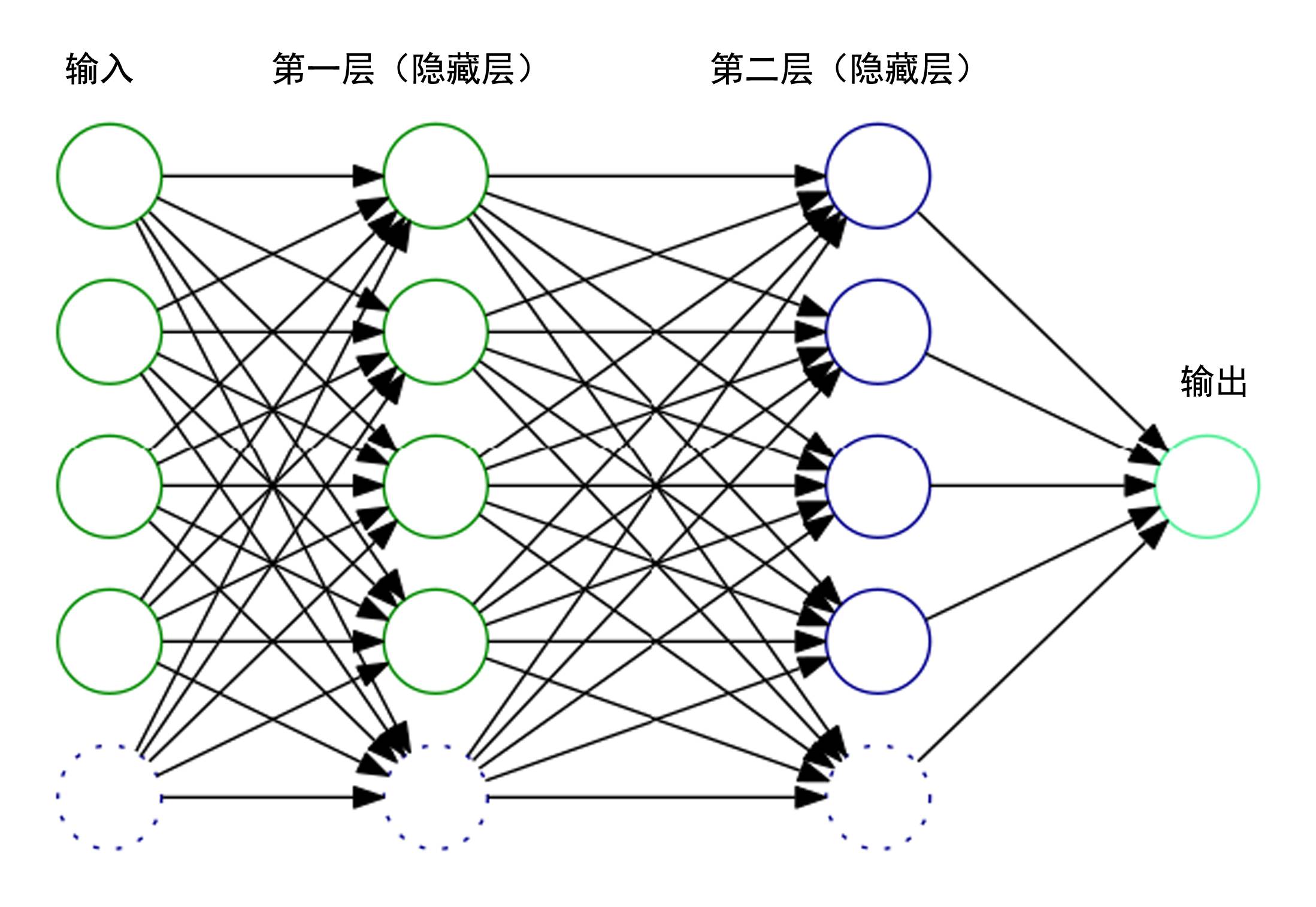
Dijkstra最短路算法

一、算法原理

    最短路问题：首先给定带权图$G=$及顶点$u$和$v$，其中每一条边$e$的权$W(e)$为非负实数，求从$u$到$v$的最短路径。

    显然，若$u{v}{i{1}}{v}{i{2}}…{v}{i{k}}v$是从$u$到$v$的最短路径，则对每一个$t(1≤t≤k)$，$u{v}{i{1}}{v}{i{2}}…{v}{i{t}}$是从$u$到$v$的最短路径，则有Dijkstra最短路算法如下：

    算法给出从起点$s$到每一点的最短路径。在计算过程中，赋予每一个顶点$v$一个标号$l(v)=(l{1}(v),l{2}(v))$。标号分永久和临时标号。在$v$的永久标号$l(v)$中，$l_2(v)$是从$s$到$v$的距离，$l_1(v)$是$s$到$v$的最短路径上$v$的前一个顶点。当$l(v)$是临时标号时，$l_1(v)$和$l_2(v)$分别是当前从$s$经过永久标号的顶点到$v$的长度最短的路径上$v$的前一个顶点和这条路径的长度

二、代码复现

1